LC Bandpass Filter Calculator
Type1(Series)
[nH]
[pF]
Type2(Shunt)
[nH]
[pF]
Formulas
$$L_{shunt_{i}} = \frac{g_i\ Z_o}{(2 \pi)^2 \ BW\ f_c}$$
$$L_{series_{i}} = \frac{BW\ f_c\ Z_o}{g_i\ (2 \pi \ f_c)^2}$$
$$C_{shunt_{i}} = \frac{BW}{g_i \ Z_o \ (2\pi \ (f_c)^2)}$$
$$C_{series_i} = \frac{g_i}{2 \pi \ BW \ Z_o}$$
$$n = \ number \ of \ LC \ pair$$
$$i = \ order \ of \ inductor \ or \ capacitor$$
$$f_c = \ cutoff \ frequency$$
$$BW = \ passband$$
$$r = \ ripple \ in \ dB$$
$$rr = \frac{r}{17.37}$$
$$g_i = \frac{2 \ a_i}{g_n}$$
$$g_i = \frac{4 \ a_{i-1} \ a_i}{b_{i-1} \ g_{i-1}}$$
$$a_i = \sin\left(\frac{(2i - 1)\pi}{2n}\right)$$
$$b_i = \ {g_n^2 \ + \sin\left(\frac{\pi i}{n}\right)^2}$$
$$g_n = \frac{e^{btn} - \ e^{-btn}}{2}$$
$$btn = \frac{log(\frac{e^{2rr} \ + \ 1}{e^{2rr} \ - \ 1})}{(2)^n}$$
Diagrams & Theory
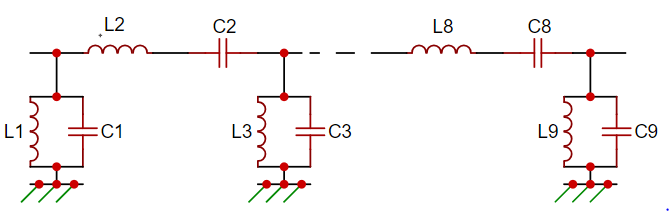
Type1 -> Series
An LC series bandpass filter is a type of electronic filter that allows signals within a certain frequency range to pass through while attenuating frequencies outside this range. It’s called a "series" filter because it uses a series combination of an inductor (L) and a capacitor (C) to achieve this filtering effect.
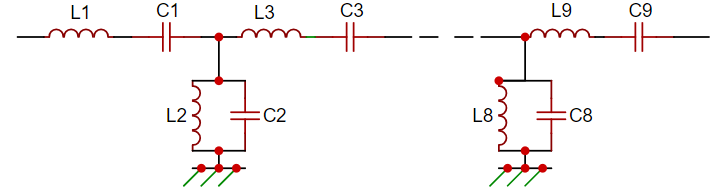
Type2 -> Shunt
An LC shunt bandpass filter is another type of bandpass filter that allows a certain range of frequencies to pass through while attenuating frequencies outside this range. The term "shunt" refers to the configuration where the inductor (L) and capacitor (C) are connected in parallel with each other and the signal path.